All News & Analysis

There is definitely a case to be made for why the Chargers should take an offensive tackle in Round 1, but some of the benefits associated with that may not be seen right away, especially if that player has to switch sides as a rookie.
Tue, 23 Apr 24 16:24:48 +0000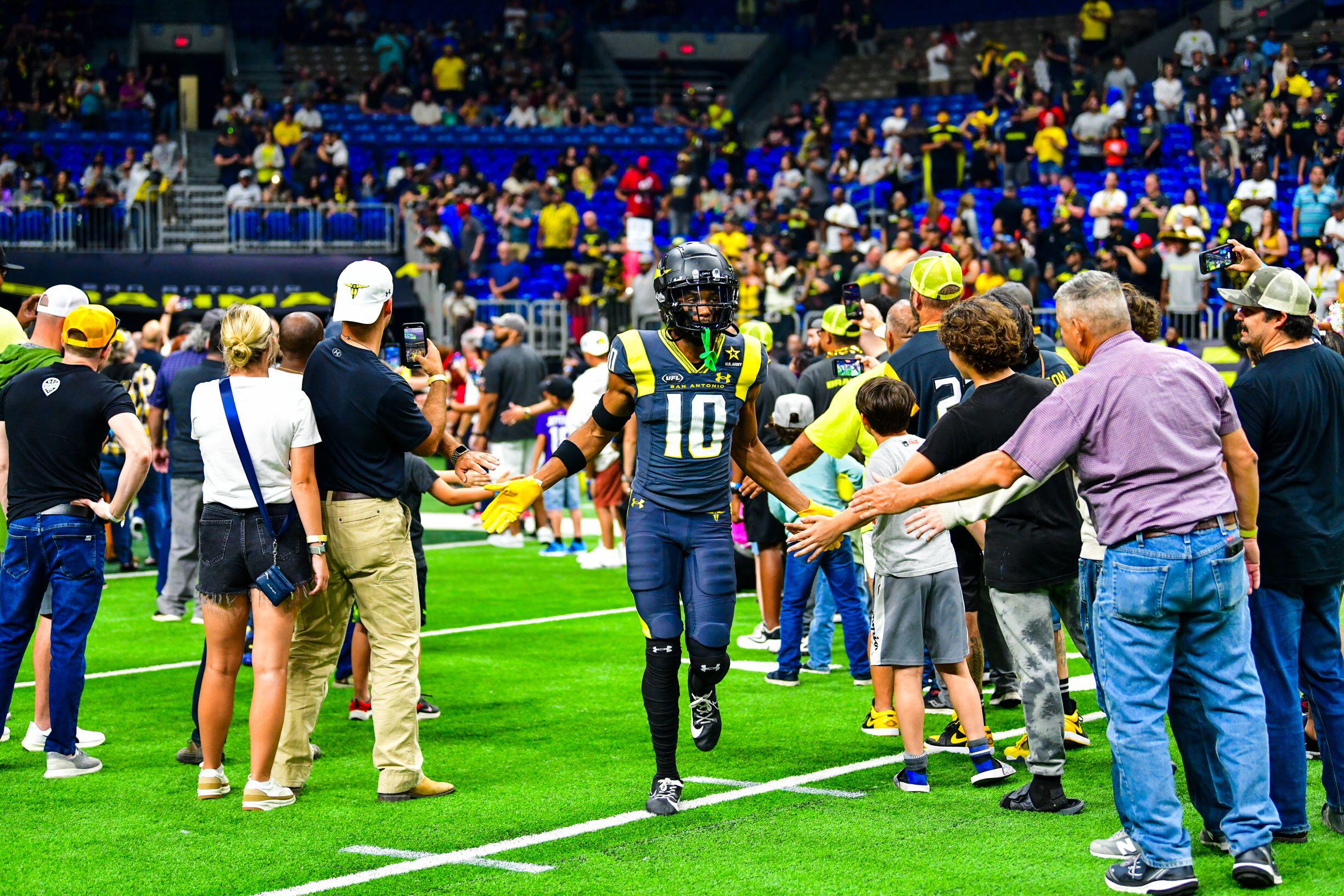
San Antonio Brahmas wide receiver Justin Smith and Memphis Showboats cornerback Quenton Meeks headline PFF's UFL Week 4 Team of the Week.
Tue, 23 Apr 24 15:30:12 +0000
Nic Bodiford reveals the 2024 NFL Draft prospects who produced the best after the catch.
Tue, 23 Apr 24 15:11:17 +0000
From Caleb Williams' top-tier arm talent to Marvin Harrison Jr.'s releases off the line of scrimmage, here are the strengths and weaknesses of PFF's top 50 draft prospects.
Tue, 23 Apr 24 14:15:42 +0000
Six quarterbacks have a shot at going in the first round of the 2024 NFL Draft, and they each have questions to answer.
Tue, 23 Apr 24 13:15:42 +0000
We dive into how the final PFF big board, which features 316 players, differs from the consensus board compiled by Arif Hasan.
Tue, 23 Apr 24 12:45:51 +0000
These 2024 NFL Draft team-prospect pairings, while not always realistic based on draft slots, make sense for both parties.
Tue, 23 Apr 24 11:45:31 +0000
Jon Macri breaks down the 2024 pre-draft rookie sleepers in fantasy football.
Tue, 23 Apr 24 11:45:11 +0000
Nic Bodiford reveals the best fantasy football landing spots for tight ends in the 2024 NFL Draft.
Tue, 23 Apr 24 11:30:31 +0000
Troy Franklin will get labeled as a one-dimensional deep threat, but there is more route-running nuance to his game than that.
Tue, 23 Apr 24 10:45:39 +0000
Kate Magdziuk breaks down the five biggest storylines ahead of the 2024 NFL Draft's first round.
Tue, 23 Apr 24 10:15:59 +0000
Zoltán Buday breaks down which NFL teams need to get it right during the 2024 NFL Draft.
Tue, 23 Apr 24 10:00:41 +0000
Rome Odunze, Drake Maye and Olumuyiwa Fashanu are prospects worth trading up for in the 2024 NFL Draft.
Tue, 23 Apr 24 09:30:41 +0000
Marcus Mosher reveals realistic landing spots for six veterans who could get moved during the 2024 NFL Draft.
Tue, 23 Apr 24 09:15:01 +0000
The Minnesota Vikings trade up for J.J. McCarthy and the Los Angeles Rams move up for Jayden Daniels in this 2024 NFL mock draft.
Tue, 23 Apr 24 09:00:49 +0000
“You're getting somebody who cares about football, who's passionate about football, who loves and studies the game at a very high level, and someone who knows what it takes to win.”
Mon, 22 Apr 24 19:15:06 +0000
Nic Bodiford identifies the best rushers, regardless of position, in the 2024 NFL Draft.
Mon, 22 Apr 24 15:44:08 +0000
The 2024 NFL Draft is finally upon us after a wild early offseason that saw dramatic moves via free agency and trades. Every team still has needs, though, so we’ll highlight what each should do during the first round this Thursday night.
Mon, 22 Apr 24 15:15:29 +0000
Could the Bills move up for a top-flight wide receiver? Will the Rams address the quarterback position in Round 1?
Mon, 22 Apr 24 14:30:04 +0000All Featured Tools
-
Our exclusive database, featuring the most in-depth collection of NFL player performance data.
Available with
PFF All News & Analysis
The latest football news, analysis, and rankings from PFF. Featuring data-driven rankings and stats for NFL, fantasy football, and the NFL Draft.

 © 2024 PFF - all rights reserved.
© 2024 PFF - all rights reserved.